The Franchot Engine of 1838

Fundamental principles.

The absolute motive power, called caloric, is independent of the agents used to carry it out (1).

It is determined only :

1. by the thermometric distance which separates the heater from which the caloric emanates, from the receptacle which absorbs it ;
2. by the quantity of this fluid available in the unit of time (by the number of calories).

In other words, the motive power of the caloric, like that of a waterfall, must be estimated by the height and the abundance of the fall.

But it is not enough, in order to make the most out of the caloric, to use it at the temperature nearest to that of its source, it is necessary to use all the degrees of its fall, it is necessary that all transport of caloric from the heater to the refrigerant, results, not from a restoration of equilibrium between distant temperatures or a direct fall, but from a dynamic change of volume in the working fluid which serves as a vehicle for the caloric .

In short :

1. use the highest caloric drop,
2. take advantage of all the degrees of the fall (2): these are the conditions of maximum useful effect for a given fuel expenditure.

If, according to our first principle, it seems that we can use indistinctly all bodies as intermediate agents (working fluid), with the same economic advantages, we recognize, when we try to put ourselves practically under the conditions of the maximum useful effect, that it is not irrelevant to use such or such a gas or vapor and that the best steam engines, for example, barely realize the 10th of the dynamic effect that one could expect from an air machine for an equal expenditure of fuel and taking into account ordinary losses of caloric in fire engines.

Indeed the steam engines in use, even the high pressure machines with expansion and condensation, do not realize, as for the height of the caloric fall, only 100° C to 120° C, that is to say the difference between the temperature of production of the steam and the temperature of the condenser; and scarcely half of the degrees of this small fall is used by the expansion

Low-pressure machines and high-pressure machines with non-condensing expansion are in conditions even more unfavorable from a theoretical point of view, since they only achieve caloric drops of 60 to 70 degrees.

And yet our furnaces give temperatures of more than 1,000 degrees, while we find in abundance, in the nature, refrigerating bodies of 10° C to 20° C. It is therefore not surprising that ordinary steam engines barely make up the 60th part of the motive power of the fuel.

The atmospheric air and the permanent gases, in general, allow to approach much more the conditions of the maximum useful effect without exceeding the restrictions of the practice.

Thus, confining ourselves, for an upper limit, to the temperature of 325° C and to that of 25° C for the lower limit, a difference which varies from 1 to 2 the pressure of a constant volume of air, we already obtain a fall of calorie of 300° C.

As to use all the degrees of this fall by a sufficient expansion, it would be difficult, even with a permanent gas, because one would fall into volume increases that our practical means do not allow us to use (3).

It is, however, of the utmost importance not to abandon the caloric, which is found almost entirely in the gas, after an expansion, that is still very incomplete. Consequently we have sought to collect, to store in some way, the sensible caloric contained in the expanded gas, in order to use it again in the contracted gas, and here is the hypothesis of which we have proposed the realization to arrive at our goal.

Preliminary operation

Alternatively, with heat borrowed from E, heat up a mass of gas in a closed vessel at a constant volume.

1st operation
Use as a driving force the expansion of this mass of air in a capacity heated by the furnace which provides it with caloric F to maintain the constant temperature during the expansion.

2nd Operation
Then chasing this mass of air under constant volume in a cold chamber by a channel whose inner surfaces successively acquire or store the borrowed caloric E which that has not been spent.

3rd Operation
Use as a driving force the contraction of the mass of air within the capacity cooled by the refrigerant which absorbs the caloric F in order to maintain the constant temperature during the reduction of volume.

4th operation
Push the mass of cold air at constant volume back into the hot chamber, making it pass through the channel in which the caloric E was deposited during the first run, so that the gas enters the hot chamber only after having recovered the caloric E.

In these four operations our conditions of maximum useful effect are well respected ; for, on the one hand, changes of volume take place under the influence of extreme temperatures, and alone occasion the expenditure of caloric ; and on the other hand the transports of temperature are made in successive degrees, step by step, that is to say without any useless fall.

Nonetheless, it is certain that the reciprocal exchanges of caloric are never complete, since they suppose a difference in temperature, however slight it may be.
Secondly in practice, radiation and conductivity losses of the substances used must be taken into account, but losses can always be reduced to negligible quantities.

The main difficulty that had to be solved so that our hypothesis became practicable, was to make the hot capacity expandable without the displacement of hot gas and to avoid its contact with any grinded rubbing surface, such as those required by the pistons, drawers and valves of the steam engines.

The apparatus which we are going to describe is of the type of those which we use to reach our goal, but by subjecting it, according to the circumstances, very important modifications.

It is generally composed of a hollow cylinder that we call a generator, which is closed by one end and terminated at the other end by an (4) ORDINARY MOBILE surface capable of externally transmitting the dynamic volume changes.

In the interior of this first cylinder, there is a second concentric cylinder called a repulsor, mobile, closed at both ends and whose outer surface is as close as possible to the inner surface of the generator.

The repulsor occupies only a portion (approximately 3/4) of the height between the fixed bottom and the movable bottom of the generator; it also communicates externally by means of a rod which serves to set it in motion.

The generator is heated on the fixed bottom side and cooled on the movable bottom side, and when a reciprocating rectilinear motion is imparted to the repulsor by means of its rod, the gas passes successively from the hot end to the cold end of the generator and vice versa, either by sliding between the concentric surfaces, or by traversing an interior canal filled with metal meshes or fragments of very divided metal. (This last mode is essential in large machines.)

Well ! Here is a fact that may surprise at first glance, but that is easily explained by the inspection of our devices ; the air that is moving in the interior of the generator suddenly takes the temperature of the capacity in which it penetrates or rather it assimilates it in the run from one capacity to another.
And this transformation of temperature is so rapid that it is impossible to perceive the slightest delay in the movement of the mercury column of the manometer, which evidently plays the role of an air thermometer, when the capacity of the generator is maintained invariable.

Now we have already been able to verify that these phenomena occur in less than half a second in a 0.4 m diameter generator, in exactly the same way as in a generator of 0.125 m ; and it is not thinkable that they present abnormalities in cylinders of larger diameter, provided that the heating surfaces, or the surfaces of transistion, are well proportioned to the mass of air that circulates in a given time.

It is conceivable that the energy of the machine, all things being equal, is due to the preliminary compression of the aeriform fluid subjected to the alternatives of hot and cold. At least we could verify this until the pressure of 6 atmospheres.

Since we can not yet give a detailed description of our devices and processes, we will sum up by saying that they are established with a view to combining and reconciling:

1. Fast temperature permutations with neutral capacity reductions (5)
2. The constancy of the volume of gas with its change of temperature
3. The constancy of temperature of the gas with its change of volume

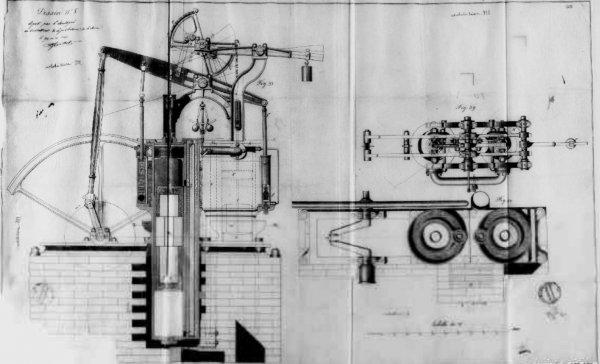
The machine on which we made our first experiments is composed of 2 vertical cylindrical generators which penetrate by their upper part in a furnace maintained approximately at the temperature of 323° C.
Their lower part contains a liquid maintained at a temperature of 20° C to 30° C. This liquid, which constitutes the movable bottom in each generator, puts them one and the other in relation through a pump body in which moves a piston ; which is the goal of the machine.

The two masses of air are moved simultaneously but inversely by the repulsors, that is to say one is heated while the other is cooled, and the pressure difference resulting in each of the generators acts immediately on the liquid surface and consequently on the piston which is moved until the equilibrium of the pressure is restored.

Then a new reverse movement of the masses of air brings the piston back to an opposite position, and so on; for it is easy to conceive that the piston is bound by arrangements well known to the shaft of a wheel to which it conveys a regular movement and that a portion of the driving force is used to put the repulsors in play, as it is practiced for the drawers of a steam engine.

To determine the motive force of this machine having two generators, it suffices to calculate the pressure in each generator, at any moment of the course of the piston, since the effective pressure on the piston consists of the pressure of the liquid contained in a generator decreased by the pressure of the liquid contained in the other generator.

We must not lose sight of the fact that we heat up the mass of air under its minimum volume and that we cool it under its maximum volume in each generator ; which supposes each mass of air moved on its corresponding sides at the moment that one considers.
We also admit that the temperatures do not vary with the volumes, assumption that is achieved by the arrangement of our devices.

Let P be the pressure to be determined on the hot air mass side,
p the pressure to be determined on the cold air mass side,
r the pressure of the air mass in the hot chamber under its maximum volume V + dn,
r' the pressure of the air mass in the cold room under the minimum volume V.

The variable volumes generated by the piston being represented by d1, d2, d3, ... dn,
a the coefficient of expansion,
t the temperature of the cold chamber,
T the temperature of the hot chamber,
C the air mass contained in neutral capacities (dead volumes) (C = V''/(1 + aB),
V'' being the volume of the neutral capacities, and B their mean temperature), we have:

P = (V + dn + C(1 + aT) / (r(V + d1 + C(1 + aT))

p = (V + C(1 + aT) / (r'(V + dn - d1 + C(1 + at))

We adopted, for our first experiences,

1+ aT = 2(1+ at),
r=r',
and therefore dn = V,
and we take r as the unit of pressure,
and V for volume unit.

Our two equations then become:

P = (2 + 2C) / (1 + d1 + 2C)

and

p = (1 +C) / (2 - d1 + C)

With the help of these two reduced formulas, we have set up a geometrical table in which appear, for 10 values of neutral capacities C, successive piston positions d1, d2, d3, and so on.

The values of C are taken as abscissa, those of d are taken as ordinates. The resulting curves represent the pressure variations, and the surfaces between the curves represent the absolute dynamic work.

In order to obtain the net work, we have drawn up a connection curve posteriorly, in order to put ourselves in the practical conditions of the movement of the repulsors, and we have carried in the last columns of the table, all the reductions made, the surface area between the curves.

Summary of the results recorded in the table of experiments

The average pressure being 1, the volume generated by the piston being 1,

doing :

C =0.1 =0.2 =0.3 =0.4 =0.5 =0.6 =0.7 =0.8 =0.9 =1

the dynamic effect of our air machine for each cubic decimetre of volume expandable or generated by the piston, is, in kilogrammeters:

=5.25 =5.105 =4.6 =4.28 =4.01 =3.81 =3.586 =2.78 =3.20 =3.10 (6)

Applications

Suppose an air machine in which C = 40 liters, the piston providing a single stroke per second and generating a volume of 100 liters.

The average pressure being 6 atmospheres, the theoretical effect of this machine would be given according to the table by 4.28 X 100 X 6 = 2568 kgm per second, that is more than 34 horses.

For this theoretical purpose a suitable coefficient of reduction should be applied for the friction and resistance of the various parts of the mechanism. Our experiments give us every reason to believe that this coefficient is not greater than that which is applied to the low-pressure steam engine.

Although our test machines leave much to be desired in terms of performance, and they are considerably different from our essential conditions, as shown in the dynamic effects table, they have already realized part of our forecasts ; or rather all that we can expect taking into account the imperfections of construction.

Enlightened today by our first experiments and by continuous studies, we are able to produce machine projects which can satisfy, in all the desired dimensions, the conditions on which we base our calculations.

For the moment we will confine ourselves to present some figures resulting from sufficiently prolonged experiments on the small machine of which we have just described.

The volume expandable or generated by the piston is 1.25 liter.
Neutral capacity is equivalent to 1 liter, or 0.8, which gives: 2.78 kgm.
The mean pressure is 4.50 atm

The number of piston strokes per minute is 70; that is 1.17stroke per second.
The theoretical dynamic effect is therefore 2.78 kgm x 1.25 liters x 4 atm x 1.17 stroke = 18.29 kgm per second.

But the useful effect transmitted to the brake is at least 8 kgm per second on average; that is to say about 44 percent, which is considerable, given the imperfection and the small size of the machine.

This useful effect results from the burning of 1/2 kg per hour of common charcoal, giving at most 6,000 calories per 1 kg, that is 3,000 calories.

But considering the smallness of our apparatus and the small thickness of the walls of the furnace, it will undoubtedly be admitted that a quarter of the absolute effect called fuel is scarcely used, since the good furnaces of the ordinary steam engines do not use little more than half.

This reduction is moreover justified by the quantity of the caloric which passes in the refrigerant.

The caloric used would therefore be represented by 3000/4 = 750 calories for one hour producing 28,800 kgm.

This quantity of heat constitutes about 1.15 kg of steam at 100° C which, in a low-pressure machine of small size, would hardly have produced a quarter of the useful effect that we obtain.

Now, if we refer to our table of dynamic effects, if we consider the lower rank occupied by our test machine, the little space of the channel in which the reciprocal exchanges of temperature take place; in a word, if we take into account the imperfection of this device executed with insufficient means, we will recognize that we are far from having achieved a maximum, and that by temporarily promising a saving of three quarters on the fuel spent by the best steam engines, we do not do unwide claims.

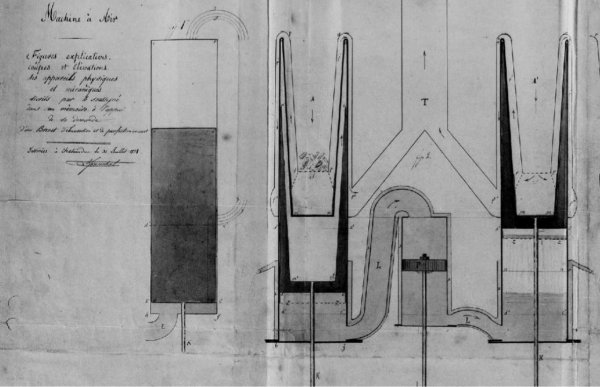
Legend

a c c, a' c' c’ generators or cylindrical shells in sheet metal whose upper part enters a furnace or stove m m heated by the hearth F.
o g g G circulation and outcome of furnace gases.
RR' refrigerant of renewed cold water, which cools externally the lower part of the generators
D b d' b' repulsors or air displacers
q q' internal liquid on which acts the air pressure
r r' small internal screen which draws a portion of the cold liquid q to disperse it in the cold room z.
L L' channel which communicates with the two generators via the pump body n n' in which moves a piston P which receives and transmits by its rod T the work resulting from the change in dynamic volume.
t t rods that serve to put the repulsors in play with a portion of the motive power given by the piston P by means of certain non-indicated transmission of motion.

The air machine compared to the Watt steam engine

 
Compared to the fuel burned
Approximately 29,000 kgm of average work per hour are produced by the burning of 1/2 kg of charcoal, containing not more than 3,000 calories, which in a regular steam boiler would have produced 2.5 kg of steam with a useful effect, in a 4 horsepower Watt machine, does not generally rise above 15,000 kgm that is to say about half of what the incomparably smaller air machine gives.

Compared to the heat spent in the refrigerant
3,200 calories are spent in the refrigerant producing 137,657 kgm. If we add approximately 500 calories for the losses due to the radiation of the refrigerant,
We will find that one sole calorie produce 137657/3700 = 37 kgm.

However, 2.5 kg of steam at 100° C represent approximately, for an effect of 15,000 kgm, 2.5 X 650 = 1625 calories.

1 calorie thus produce 15000/1625 = 9.23 kgm, that is to say a quarter of what gives the air machine.

Nota

The difference observed between the two propositions determined above is evident from the fact that 55 per cent of the fuel used as in the furnaces of large steam boilers was implicitly assumed in the first comparison. While it is probable that the furnace of the air-machine, because of its smallness, the small thickness of its walls, its isolation, etc., uses little more than 25 percent of the fuel.

(1) We intend to apply these principles only to gases and vapors.
(2) These two propositions are set forth in a work entitled Reflections on the Powerful Power of Fire; by S. Carnot. Paris, 1821. The terms degrees have no absolute meaning here.
(3) According to calculations recorded in the work of S. Carnot mentioned above, the air should be doubled to twice its original volume to cool it by only 80° C, and to 14 times its original volume to cool it to 300 ° C.
(4) Principal distinctive character
(5) We give the name of neutral or detrimental capacities to all internal cavities containing gas which can not be expelled by the repulsor (these are dead volumes). This is the case of the channel for transferring air. These capabilities greatly weaken the engine's energy, as we can see from our formula, and the inspection of the dynamic effects table that we have drawn up, and which is its geometric translation.
(6) The number 2.78 which corresponds to 0.8 is attenuated, because it applies to our first test machine, whose raepulsors move too slowly.

Franchot Hot Air Engine of his 1838 patent

In 1833 Franchot patented a Hot Iar Engine that received several addition.

Working principle

Engine elevation